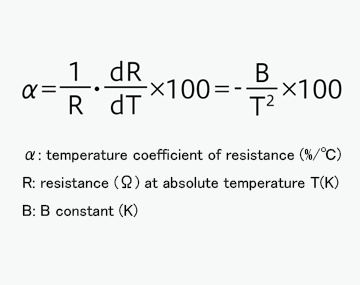- TOP
- Technical Information
Technical Information
The king of temperature sensors with a negative temperature coefficient (NTC)
A thermistor is a thermally sensitive element composed of semiconductive fine ceramics
The name thermistor comes from “a thermally sensitive resistor,” and its resistance drastically changes with temperature. The resistance of ordinary materials rises slightly as temperature rises, whereas NTC (negative temperature coefficient) thermistors exhibit a sharp decrease in resistance. Thermistors manufactured and supplied by Shibaura are all NTC thermistors.
The following descriptions are applicable only to NTC thermistors.
Thermistors are made from several transition metal oxides, primarily of Mn, Ni and Co, sintered into a fine ceramic body.
Shibaura’s thermistors cover a full range of temperatures from -50 to +500℃ that is required for daily temperature control. Our compact, stable and highly sensitive thermistors are used in large quantities as temperature sensors and for temperature compensation in many fields such as home appliances and industrial equipment.
NTC Thermistor Electrical Conductivity
It is generally known that as the temperature of a metal increases, its resistance also increases.
Metals have many free electrons. The ease with which electricity flows is equivalent to the ease with which free electrons can travel. As the temperature increases, the vibration of metal atoms becomes more intense and this interferes with the travel of the free electrons, thus making it difficult for electricity to flow and increasing resistance.
In contrast, NTC thermistors do not have many free electrons.
This means it is difficult for electricity to flow at around room temperature when compared to metals.
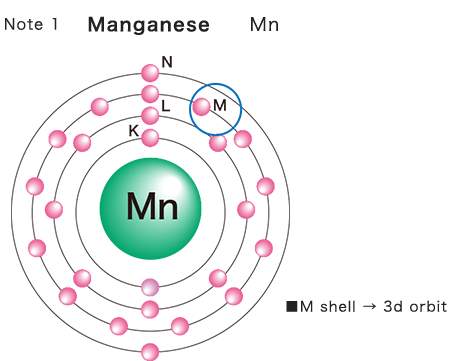
Thermistors are generally known to involve the transfer of 3d electrons in Mn. *Note 1
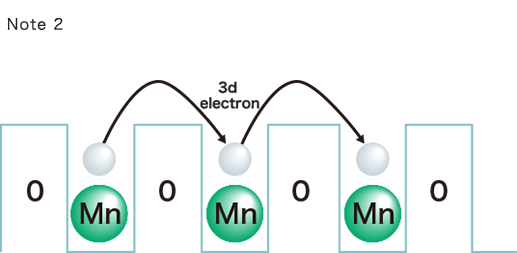
Electrical conduction in NTC thermistors is due to the movement of two carriers: free electrons and holes. When an electron (i.e. a 3d electron in Mn) enters a hole, it immediately moves to the next adjacent hole. Repetition of this movement generates the flow of electricity. This is known as “hopping conduction”. *Note 2
At low temperatures, there are fewer free electrons and their movement is sluggish, so it is difficult for electricity to flow and resistance is high. As the temperature rises, the number of carriers increases and the travel (hopping) of electrons is assisted by thermal oscillations, which makes it easier for electricity to flow.
This electrical conduction, which is different from that of metals, gives NTC thermistors their characteristic of decrease in resistance as temperature rises, and various characteristics can be created depending on the materials combined and the ratio at which they are mixed.
Physical properties of NTC thermistors
Four constants that determine the characteristics of a thermistor
The characteristics of a thermistor is basically determined by four constants;
resistance R, B constant B, thermal dissipation constant δ, and thermal time constant τ.
Details for each characteristic here
The resistance of a thermistor is defined in the standard JIS C 5602 as follows:
“The DC resistance value of a thermistor when measured at a specified temperature with sufficiently low power dissipation where its resistance change due to self-heating is negligible as compared to the overall error in measurements.”
Shibaura measures the resistance of thermistors using standardized current values and in-house developed high precision thermostatic baths.
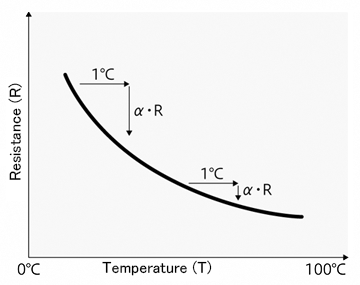
Shibaura’s thermistors are all NTC thermistors and their resistance lowers as temperature rises.
The relationship between resistance R and absolute temperature T can be approximated by the following equation.
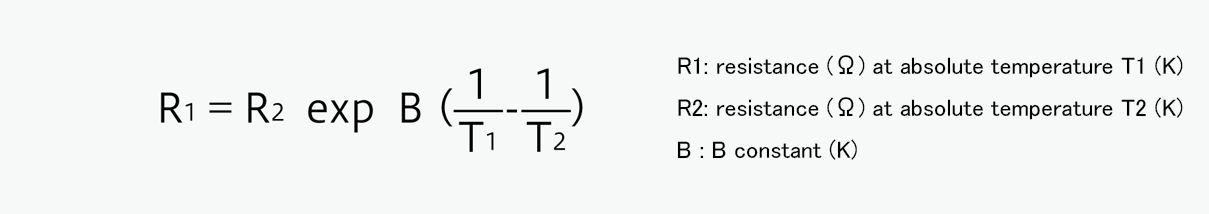
For a desirable circuit design, it is recommended to select a thermistor that exhibits the resistance within a range from 100Ω to 100kΩ for a usage temperature range.
Shibaura offers a variety of options to be selected for your specific thermistors.
The resistance can be varied by changing the size of a thermistor chip.
We are ready to customize any of our products in order to fulfill your demands.
The B constant expresses a degree of thermistor sensitivity (change rate of its resistance) to temperature changes.
The change rate can also be expressed by the gradient of a line. The larger the gradient, the higher the sensitivity.
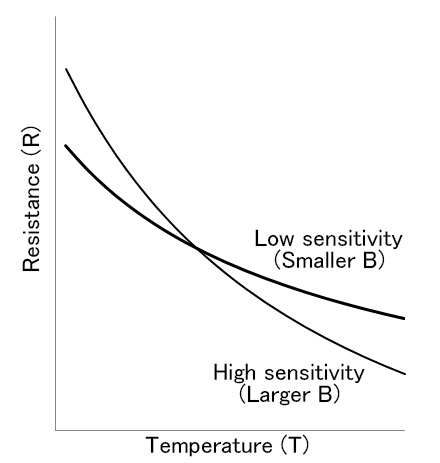
The B constant is derived from the following equation using a change rate in resistance between two given temperatures.
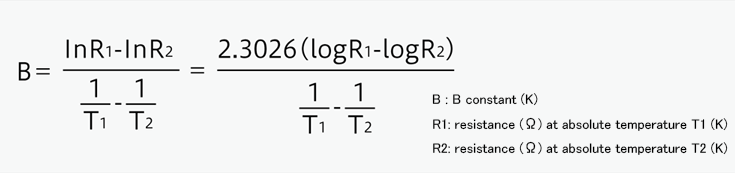
The B constant, unlike the resistance, cannot be varied by changing the chip size, but is determined by the material composition of a thermistor chip.
Additionally, in general, the larger the B constant, the higher the resistance of a thermistor will be. Therefore, the combination of resistance and B value has a limitation.
It is, for example, very difficult to create a thermistor which has a very high resistance and a very small B value.
Shibaura has a vast array of combinations of resistances and B values, and you can see a part of the whole data on our website and product catalogue.
We also support you with creating an original B value.
Here is an example of a B value (B0/100) calculation.

The thermal dissipation constant δ indicates the amount of power required for a thermistor to heat itself up by 1℃ when it is energized in still air (mW/℃).
When a power W is applied to the thermistor at an ambient temperature Ta and the temperature of the thermistor finally reaches a temperature T, the following equation is established.

Applying a power equivalent to the thermal dissipation constant makes a thermistor heat itself up by 1℃. This causes an error between the measured and the actual ambient temperatures.
Therefore, it is necessary to design circuitry to minimize the power to be applied so that measurement errors caused by thermistor’s self-heating are eliminated.
The thermal dissipation constant δ is determined by a balance between “self-heating” and “heat dissipation.” As a result, it varies substantially depending on the thermistor’s surroundings.
Placing materials that have a high thermal conductivity around the thermistor promotes heat release and increases the constant δ.
On the contrary, the construction allowing heat to accumulate decreases it. Therefore, it is essential to select appropriate materials in assembling your thermistor.
It is also important, after assembling your thermistor, to measure the constant δ in its operation environment (air, water, oil, hot plate etc.) to see that the constant meets your requirement.
The thermal time constant indicates a time required for a thermistor to respond to a change in its ambient temperature.
When the ambient temperature is changed from T1 to T2, the relationship between the time elapsed during the temperature change t (sec.) and the thermistor temperature T can be expressed by the following equation.
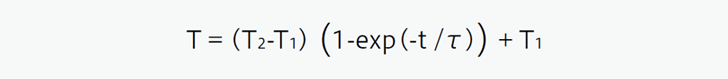
τ (tau in sec.) in the equation denotes the thermal time constant.
Now, assuming t and τ (tau) are equal (t = τ), the equation can be expressed as follows.
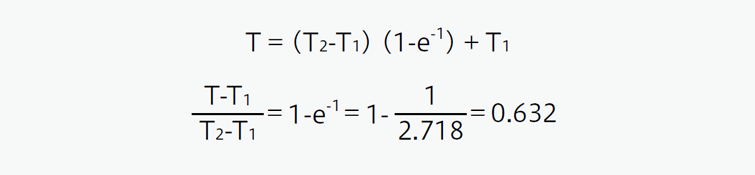
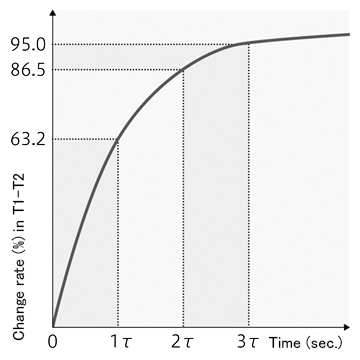
This shows that the constant τ (sec.) is defined as a time for the thermistor to reach 63.2% of the total difference between its initial and final body temperatures.
The thermistor body temperature does not reach its ambient temperature when a time period defined by τ is elapsed.
The temperature change rate at n times the constant τ (sec.) is as follows, showing that the thermistor body temperature reaches its ambient temperature approximately within 7 times the constant.
τ = 63.2%, 2τ = 86.5%, 3τ = 95.0%, ・・・・ 7τ ≒ 100%
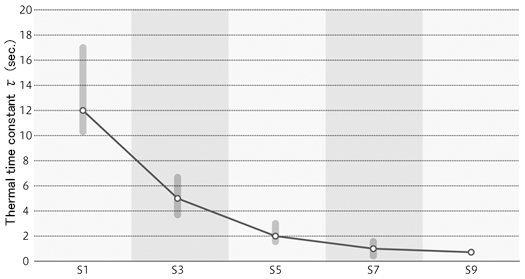
Generally, the smaller the size of the thermistor, the faster the thermal response, and thus the smaller the constant τ will be. The constant varies significantly depending on thermistor assemblies. It is necessary to select materials having a high thermal conductivity considering the environment where the thermistor is used.
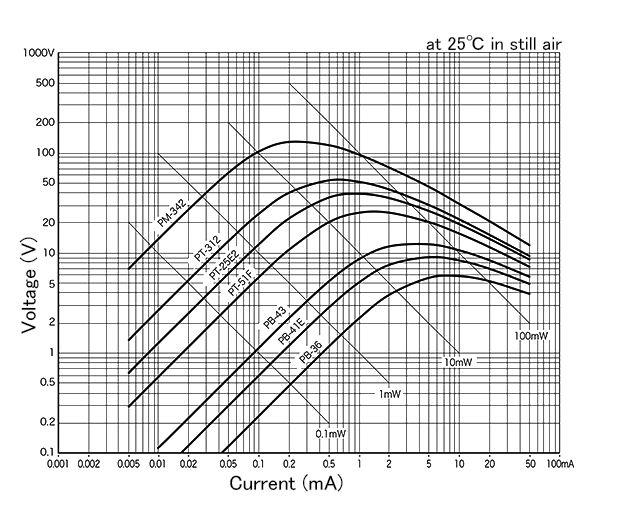
The current - voltage characteristics describes the voltage change as the current flow through a thermistor varies.
I-V curves of NTC thermistors are characterized in that the voltage rises linearly as the current rises. However, the voltage begins to decrease after achieving its peak at a certain current value.
A thermistor begins self-heating when a current is applied, and the amount of heat generated by the thermistor becomes larger as that of current flow increases.
While the heat generation is small, the heat release from the surface and lead wires of the thermistor is large. Thus, the thermistor body temperature will not change and so too its resistance. The current and voltage are directly proportional to each other according to Ohm’s Law.
However, once the amount of heat generation becomes larger than that of heat release, the thermistor body temperature rises, its resistance lowers, and the proportional relationship between current and voltage is lost. Then the voltage gradually decreases after achieving its peak at a certain point.
The chart below shows the I-V characteristics of different thermistor elements. It is important to use a thermistor within the range where a line is straight and self-heating has little effect on the resistance.
Using voltages over the peaks shown on the chart may bring the thermistors into “a runaway mode” where they glow and break down in a short time. Particular attention should be given to voltages that will be applied.
The temperature coefficient of a thermistor denotes the rate of change of thermistor resistance per 1℃ and is commonly expressed in %/℃.
The coefficient α is defined by 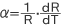
Here, the equation to approximate the relationship between resistance R and absolute temperature T (see the Section "Resistance") is differentiated for temperature T and substituted into the above equation.
Then the following equation is obtained.
The coefficient α of a thermistor with its B = 3400K and T = 293.15K (20℃), for example, can be determined as follows.
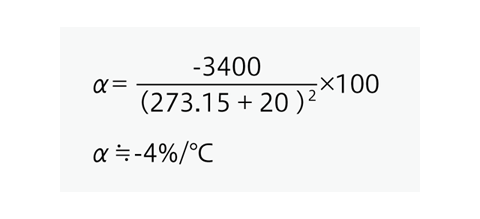
The negative sign of the coefficient α indicates that the thermistor resistance decreases with increasing temperature.
Metals and alloys, in general, raise their resistance as temperature rises. Their temperature coefficients of resistance, for example, are 0.4%/℃ (gold), 0.39%/℃ (platinum), and iron and nickel are relatively larger with 0.66%/℃ and 0.67%/℃, respectively. Thermistors, as compared with these metals, vary their resistance significantly with a small temperature change. Therefore, thermistors are suitable for precise temperature measurements and controlling the temperature by using slight differences in temperature.
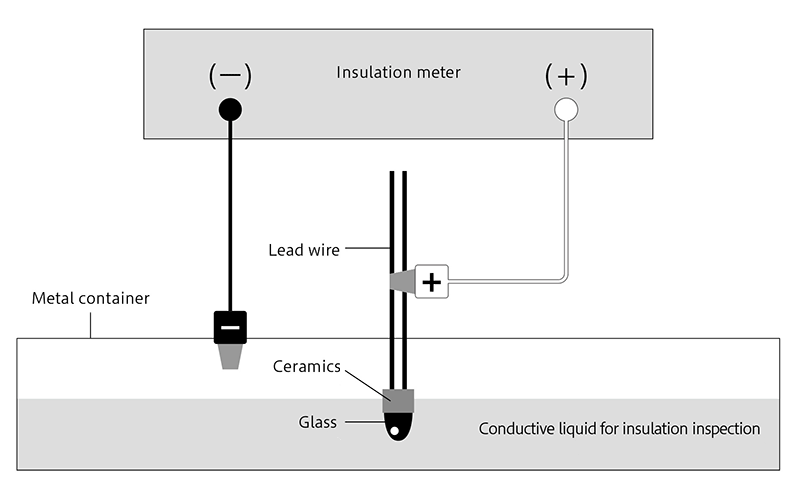
The insulation resistance of a thermistor element is measured between its lead wires and glass. It is essential that a thermistor provides good electrical insulation to secure its durability. Shibaura carries out 100% inspection on all products (except PSB-N, RB1-N and KG) by measuring the insulation resistance of each element in manufacturing processes.
The figure below shows the measuring method.
A metal container is filled with conductive liquid. A thermistor is immersed in the liquid in such a way that its glass is submerged below the liquid surface. (For NS elements, the liquid level is on the ceramics.)
The positive pole of the insulation meter is connected to the thermistor lead wires, and the negative pole to the metal container, and the resistance between the lead wires and glass is measured.